二阶系统 稳定,深入解析二阶系统的稳定性

深入解析二阶系统的稳定性

在自动控制理论中，二阶系统因其简洁的数学模型和丰富的物理意义而被广泛应用。本文将深入探讨二阶系统的稳定性，分析其稳定性的影响因素，并介绍几种常用的稳定性分析方法。

一、二阶系统的基本概念

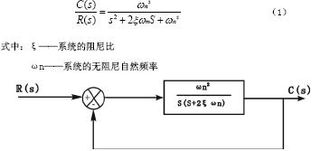
二阶系统是指具有两个独立能控或能观状态变量的线性时不变系统。其数学模型通常表示为二阶微分方程，形式如下：

[ ddot{x}(t) + 2zetaomega_ndot{x}(t) + omega_n^2x(t) = 0 ]

其中，( x(t) ) 是系统的状态变量，( omega_n ) 是系统的自然频率，( zeta ) 是阻尼比。该方程描述了系统在受到扰动后的动态响应过程。

二、二阶系统的稳定性分析

二阶系统的稳定性主要取决于其自然频率 ( omega_n ) 和阻尼比 ( zeta )。根据 ( zeta ) 的不同取值，二阶系统可以分为以下几种情况：

1. 欠阻尼系统（( 0

欠阻尼系统具有一个实部为负的复数极点，其动态响应表现为衰减振荡。随着时间推移，系统最终会趋于稳定状态。欠阻尼系统的稳定性可以通过以下条件判断：

[ text{Re}(p) 2. 临界阻尼系统（( zeta = 1 )）

临界阻尼系统具有两个相等的实部为负的极点，其动态响应表现为无振荡的衰减过程。临界阻尼系统是稳定的，但响应速度较慢。

3. 过阻尼系统（( zeta > 1 )）

过阻尼系统具有两个实部为负的实数极点，其动态响应表现为无振荡的衰减过程。过阻尼系统是稳定的，但响应速度较慢。

4. 负阻尼系统（( zeta

负阻尼系统具有一个实部为正的复数极点，其动态响应表现为增长振荡。负阻尼系统是不稳定的，系统会逐渐偏离平衡状态。

三、二阶系统的稳定性分析方法

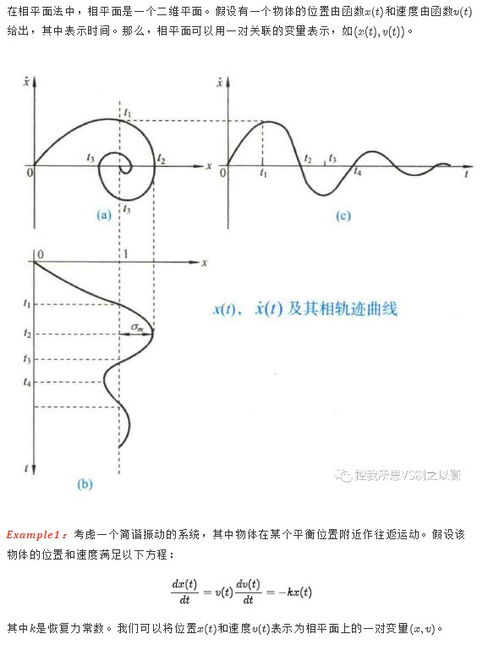
为了更直观地分析二阶系统的稳定性，可以采用以下几种方法：

1. 阶跃响应法

阶跃响应法是通过观察系统在阶跃输入下的动态响应来判断其稳定性。对于欠阻尼系统，阶跃响应表现为衰减振荡；对于临界阻尼和过阻尼系统，阶跃响应表现为无振荡的衰减过程。

2. Nyquist图法

Nyquist图法是通过绘制系统开环传递函数的Nyquist曲线来判断其稳定性。如果Nyquist曲线不包围(-1, j0)点，则系统是稳定的；否则，系统是不稳定的。

3. Bode图法

Bode图法是通过绘制系统开环传递函数的幅频特性和相频特性来判断其稳定性。如果系统的幅频特性和相频特性满足一定的条件，则系统是稳定的。

四、结论

二阶系统的稳定性与其自然频率和阻尼比密切相关。通过分析二阶系统的稳定性，可以设计出满足实际需求的控制系统。本文介绍了二阶系统的稳定性分析方法，为实际工程应用提供了理论依据。