2自旋系统,自旋系统的基本概念

自旋系统的基本概念

自旋系统是量子力学中的一个重要概念，它描述了微观粒子（如电子、原子核等）的角动量性质。在经典物理学中，角动量是描述物体旋转状态的物理量，而在量子力学中，角动量被量子化，即只能取特定的离散值。自旋系统就是研究这些量子化的角动量及其相关性质的理论体系。

自旋量子数的定义

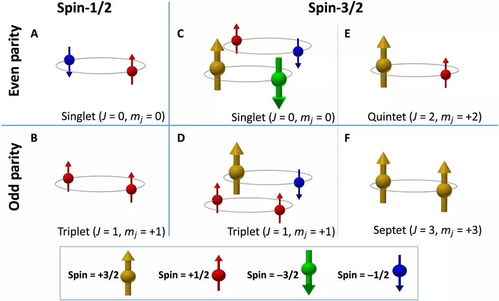
自旋量子数是描述自旋系统角动量大小的量子数，用符号s表示。自旋量子数可以是整数或半整数，这取决于粒子的自旋性质。对于整数自旋量子数，粒子被称为玻色子；对于半整数自旋量子数，粒子被称为费米子。例如，电子的自旋量子数为1/2，因此它是一个费米子。

自旋态的表示

自旋态是描述自旋系统状态的量子态，可以用自旋波函数来表示。自旋波函数通常用符号|ψ?表示，其中ψ是波函数的复数表示。对于自旋量子数为s的粒子，其自旋波函数可以写成|↑?和|↓?两种状态，分别对应自旋向上和自旋向下的状态。这两种状态是正交的，即它们的内积为0。

自旋系统的相互作用

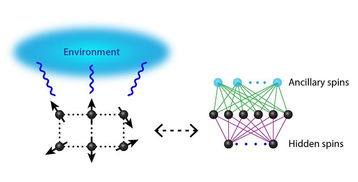
自旋系统中的粒子可以通过自旋交换相互作用。这种相互作用在固体物理、量子信息等领域中具有重要意义。自旋交换相互作用可以用Heisenberg模型来描述，该模型是一个经典的量子力学模型，描述了自旋系统中的粒子之间的相互作用。在Heisenberg模型中，自旋交换相互作用可以用一个交换积分J来表示。

自旋系统的对称性

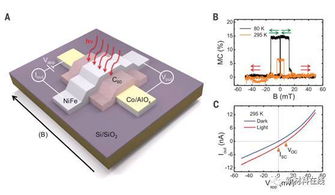
自旋系统具有多种对称性，这些对称性在量子力学中起着重要作用。例如，自旋系统的宇称对称性是指自旋波函数在空间反演下的不变性。此外，自旋系统还具有时间反演对称性和电荷共轭对称性等。这些对称性在自旋系统的物理性质和实验观测中都有体现。

自旋系统的应用

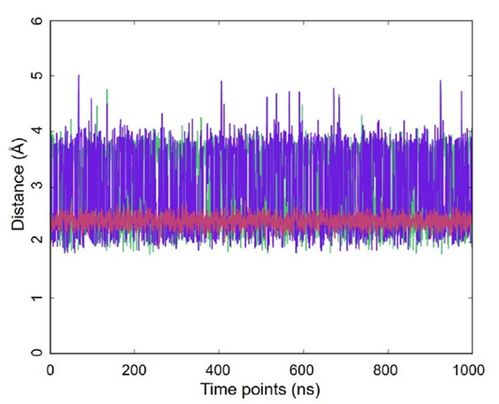
自旋系统在多个领域都有广泛的应用。在固体物理中，自旋系统的研究有助于理解磁性材料的性质和磁共振现象。在量子信息领域，自旋系统是量子计算和量子通信的基础。例如，量子比特可以用自旋系统的状态来表示，而量子逻辑门可以用自旋交换相互作用来实现。

自旋系统的实验研究

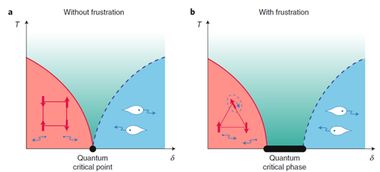
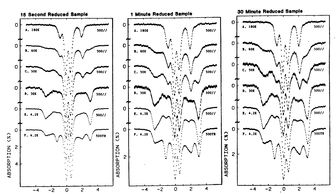
自旋系统的实验研究主要依赖于核磁共振（NMR）和冷原子物理等技术。通过这些技术，科学家可以制备和操控自旋系统，从而研究其性质。例如，通过NMR技术，可以测量自旋系统的磁化率和磁共振频率等物理量。在冷原子物理中，通过激光冷却和蒸发冷却技术，可以制备出低温度下的原子气体，从而实现自旋系统的精确操控。

自旋系统的未来展望

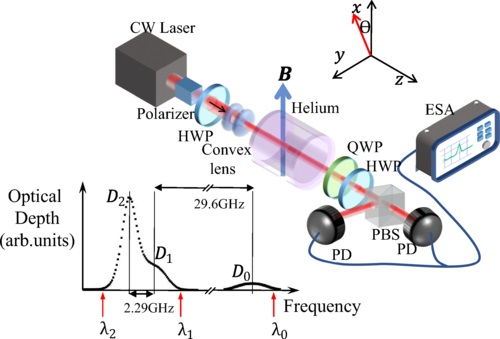
随着量子信息技术的快速发展，自旋系统的研究将越来越重要。未来，自旋系统的研究将主要集中在以下几个方面：一是提高自旋系统的操控精度，以实现更复杂的量子计算和量子通信任务；二是探索新的自旋系统材料，以拓展量子信息技术的应用范围；三是研究自旋系统与其他物理系统的耦合，以开发新的量子物理现象和应用。

通过以上内容，我们可以看到自旋系统在量子力学、固体物理、量子信息等领域的重要性，以及其在实验研究中的广泛应用和未来发展的广阔前景。