二阶系统伯德图,二阶系统伯德图解析与应用

你知道吗？在控制系统的世界里，有一个超级酷的工具，它就像是一面镜子，能让我们看到系统在不同频率下的“舞蹈”。这个神奇的宝贝，就是二阶系统的伯德图！今天，就让我带你一起，揭开这神秘面纱，探索二阶系统伯德图的奥秘吧！

一、伯德图：揭秘系统频率的“舞蹈”

想象你站在一个巨大的舞池中央，周围是五彩斑斓的灯光，音乐在耳边回荡。突然，一个舞者出现在你面前，他随着音乐的节奏，时而优雅旋转，时而快速跳跃。这就是二阶系统伯德图带给我们的感觉——它让我们看到了系统在不同频率下的动态变化。

伯德图由两部分组成：幅度图和相位图。幅度图展示了系统增益与频率的关系，就像舞者的步伐；相位图则描绘了系统相位滞后与频率的变化情况，就像舞者的姿态。这两者结合在一起，就像是一场精彩的舞蹈表演，让我们对系统的动态性能有了更深入的了解。

二、绘制伯德图：MATLAB带你飞

想要绘制二阶系统的伯德图，MATLAB可是我们的得力助手！下面，就让我带你一步步完成这个任务。

1. 定义二阶系统的传递函数：首先，我们需要定义一个二阶系统的传递函数。比如，一个典型的二阶系统传递函数可以表示为：

```

G(s) = ωn^2 / (s^2 + 2ζωns + ωn^2)

```

其中，ωn 是自然频率，ζ 是阻尼比。

2. 绘制伯德图：在MATLAB中，我们可以使用 `bodeplot` 函数来绘制伯德图。以下是一个示例代码：

```matlab

wn = 10; % 自然频率

zeta = 0.5; % 阻尼比

G = tf(wn^2, [1, 2zetawn, wn^2]); % 定义传递函数

bodeplot(G); % 绘制伯德图

```

运行这段代码，你就能看到一个漂亮的伯德图出现在你的眼前。

三、解读伯德图：揭秘系统的“性格”

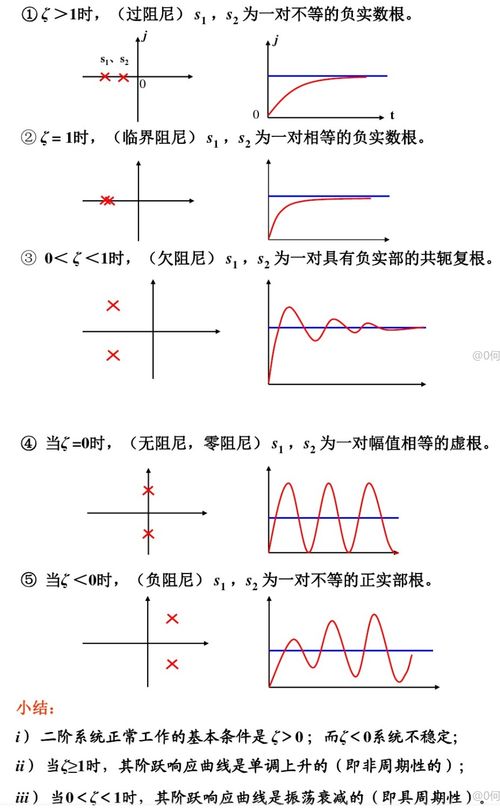
伯德图中的信息量可不少，让我们一起来看看如何解读它。

1. 幅度图：幅度图展示了系统增益与频率的关系。在幅度图中，我们可以看到以下特点：

- 当频率较低时，系统增益较高，这意味着系统对低频信号响应较好。

- 当频率较高时，系统增益逐渐下降，这意味着系统对高频信号响应较差。

2. 相位图：相位图展示了系统相位滞后与频率的关系。在相位图中，我们可以看到以下特点：

- 当频率较低时，系统相位滞后较小，这意味着系统对低频信号相位影响较小。

- 当频率较高时，系统相位滞后逐渐增大，这意味着系统对高频信号相位影响较大。

通过分析幅度图和相位图，我们可以了解系统的动态性能，比如稳定性、响应速度和频率选择性等。

四、伯德图的应用：控制系统的“医生”

伯德图在控制系统设计中有着广泛的应用，就像一位经验丰富的医生，帮助我们诊断和解决问题。

1. 系统稳定性分析：通过分析伯德图，我们可以判断系统是否稳定。如果相位裕量和增益裕度都大于零，那么系统是稳定的。

2. 系统性能优化：通过调整系统参数，我们可以优化系统的性能。比如，我们可以通过调整阻尼比来改善系统的响应速度和超调量。

3. 系统比较：通过绘制多个系统的伯德图，我们可以比较它们的性能，从而选择最优的系统。

五、：伯德图——控制系统的“舞者”

通过本文的介绍，相信你已经对二阶系统伯德图有了更深入的了解。伯德图就像一位舞者，用它的步伐和姿态，向我们展示了系统的动态性能。在控制系统的世界里，伯德图是一位不可或缺的“医生”，帮助我们诊断和解决问题。让我们一起，用伯德图这把神奇的“舞者之剑”，探索控制系统的奥秘吧！