非线性系统 平衡点,非线性系统平衡点分析与应用探讨

你知道吗？在复杂的世界里，有些东西就像捉迷藏一样，让人捉摸不透。今天，咱们就来聊聊这个神秘的家伙——非线性系统，还有它那让人好奇的平衡点。

非线性系统的魅力

想象你手中有一根橡皮筋，轻轻一拉，它就会变长。但是，如果你拉得太猛，它就会突然断裂。这就是非线性系统的特点，它们的行为不是简单的线性关系，而是复杂多变，有时候甚至让人摸不着头脑。

非线性系统无处不在，从自然界到人类社会，从简单的摆动到复杂的生态系统，都离不开它们的身影。比如，天气变化、股市波动、人口增长等，都是非线性系统的典型例子。

平衡点：非线性系统的秘密花园

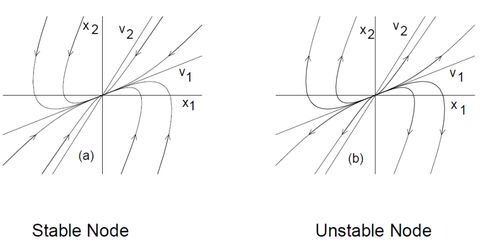
在非线性系统中，有一个特别的地方，那就是平衡点。平衡点就像是系统的“家”，它代表着系统在某个时刻的稳定状态。简单来说，就是系统在这个点上，不会因为外界的干扰而改变自己的状态。

平衡点有稳定和不稳定之分。稳定的平衡点就像一个安静的湖面，无论风吹雨打，它都能保持平静。而不稳定的平衡点则像一颗定时炸弹，稍有不慎，就会引发一场“爆炸”。

那么，如何判断一个平衡点是稳定还是不稳定呢？这就需要用到一种神奇的方法——后继函数法。

后继函数法：揭开平衡点的神秘面纱

后继函数法是一种基于线性化系统模型的方法，它通过近似将非线性系统线性化，来评估平衡点的稳定性。

使用后继函数法，我们可以按照以下步骤来分析平衡点的稳定性：

1. 确定平衡点：首先，我们需要找到非线性系统的平衡点。这可以通过解系统的微分方程来实现。

2. 线性化系统：在平衡点附近，我们将非线性系统线性化，得到一个线性系统模型。

3. 计算后继函数：根据线性系统模型，我们计算后继函数。后继函数描述了系统在平衡点附近的状态变化。

4. 分析后继函数：通过分析后继函数的性质，我们可以判断平衡点的稳定性。如果后继函数的值始终小于1，那么平衡点是稳定的；如果后继函数的值始终大于1，那么平衡点是不稳定的。

5. 验证结果：需要注意的是，后继函数法是基于线性化系统模型进行的，它可能无法准确描述非线性系统的行为。因此，我们需要进一步验证和分析，以确保结果的准确性。

相平面法：另一种视角看平衡点

除了后继函数法，我们还可以使用相平面法来分析平衡点的稳定性。

相平面法是一种将系统的状态变量表示为二维平面上的轨迹的方法。通过观察轨迹的形状和特性，我们可以推断系统的稳定性、周期性或者混沌行为。

在相平面上，平衡点通常表现为一个点。如果轨迹在平衡点附近逐渐靠近这个点，那么平衡点是稳定的；如果轨迹在平衡点附近逐渐远离这个点，那么平衡点是不稳定的。

非线性系统的挑战与机遇

非线性系统的复杂性和不确定性，给我们的研究带来了巨大的挑战。但是，正是这种复杂性，也为我们提供了无限的机遇。

通过深入研究非线性系统，我们可以更好地理解自然界的规律，为人类社会的发展提供新的思路。比如，在环境保护、能源利用、交通规划等领域，非线性系统的研究都具有重要意义。

非线性系统和平衡点就像一个神秘的谜团，等待着我们去探索。让我们一起揭开这个谜团，走进非线性世界的奇妙之旅吧！