二阶系统阶跃响应,性能与稳定性探究

你知道吗？在控制系统的世界里，有一种系统特别引人注目，它就是二阶系统。今天，咱们就来聊聊这个二阶系统的小宝贝——阶跃响应。想象你给这个系统一个突然的“惊喜”，它会怎么反应呢？是不是觉得有点好奇？那就跟着我一起，揭开二阶系统阶跃响应的神秘面纱吧！

一、二阶系统，你了解多少？

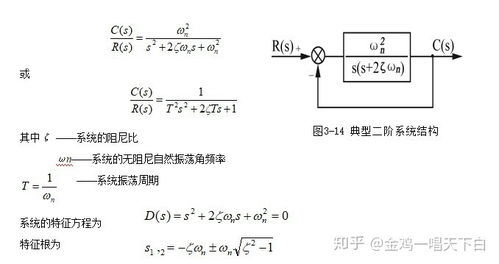
二阶系统，听起来是不是有点高大上？其实，它就是由二阶微分方程描述的系统。别看它名字里有个“二阶”，但它在控制工程中的应用可广泛了。很多看起来复杂的高阶系统，在特定条件下，都可以简化成二阶系统来研究。就像一个复杂的拼图，二阶系统就是那个关键的拼块。

二阶系统的传递函数长这样：\\( G(s) = \\frac{1}{s^2 + 2\\zeta\\omega_n s + \\omega_n^2} \\)。这里的 \\( \\zeta \\) 是阻尼系数，\\( \\omega_n \\) 是无阻尼自然频率。这两个参数，就像是二阶系统的DNA，决定了它的性格和特点。

二、阶跃响应，系统的小情绪

说到阶跃响应，那可就是二阶系统的小情绪了。当系统受到一个突然的阶跃输入时，它的输出会怎样变化呢？这就得看 \\( \\zeta \\) 和 \\( \\omega_n \\) 的值了。

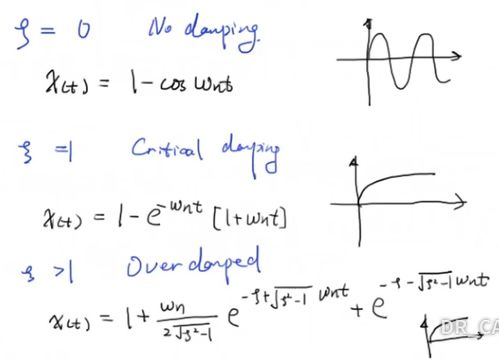
1. 欠阻尼系统：当 \\( 0 < \\zeta < 1 \\) 时，系统就像一个活泼的孩子，收到“惊喜”后会兴奋地振荡一段时间，然后慢慢平静下来。这个过程，就像是荡秋千，先荡起来，再慢慢停下来。

2. 临界阻尼系统：当 \\( \\zeta = 1 \\) 时，系统就像一个稳重的成年人，收到“惊喜”后会迅速平静下来，没有一丝波动。这个过程，就像是平静的湖面，收到石头后，水花四溅，但很快又恢复了平静。

3. 过阻尼系统：当 \\( \\zeta > 1 \\) 时，系统就像一个沉稳的老人，收到“惊喜”后会慢慢平静下来，但没有任何波动。这个过程，就像是扔进石头的水池，水花很小，很快就消失了。

三、实验大揭秘：MATLAB带你飞

想要更直观地了解二阶系统阶跃响应？那就用MATLAB来模拟一下吧！MATLAB这个强大的工具，可以帮助我们轻松地搭建系统模型，观察不同参数下的阶跃响应曲线。

在MATLAB中，我们可以通过改变 \\( \\zeta \\) 和 \\( \\omega_n \\) 的值，来观察系统阶跃响应的变化。你会发现，随着 \\( \\zeta \\) 的增大，系统的响应速度会变慢，振荡幅度也会减小；而随着 \\( \\omega_n \\) 的增大，系统的响应速度会变快，振荡幅度也会增大。

四、：二阶系统阶跃响应，你值得拥有

通过这篇文章，相信你对二阶系统阶跃响应有了更深入的了解。它就像一个多面的性格，既有活泼的欠阻尼系统，也有稳重的临界阻尼系统和过阻尼系统。而MATLAB这个工具，则可以帮助我们更好地观察和分析这些性格。

所以，下次当你遇到二阶系统阶跃响应的问题时，不妨拿出MATLAB来试试吧！相信它会给你带来意想不到的惊喜。毕竟，二阶系统阶跃响应，你值得拥有！