二次系统 稳态误差,二阶系统稳态误差产生的原因

二次系统 稳态误差目录

二次系统 稳态误差

二阶系统稳态误差产生的原因

二型系统稳态误差

系统稳态误差的计算例题

二次系统 稳态误差

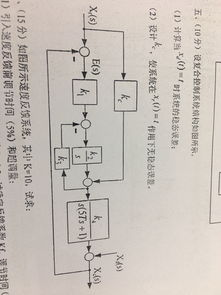
分析和优化二阶系统的稳定误差。

随着自动化技术的不断发展，二次系统在工业控制领域得到越来越广泛的应用。二次系统的稳态误差是测量系统性能的重要指标之一。本论文详细解析二次系统稳态误差的概念，影响因素和优化策略。

标签:二次系统，稳定误差，概念解析

系统稳定误差的概念。

稳定误差是指系统稳定时的输出量与期望值的偏差。在二次系统中，稳定误差主要表现为输出量的稳定偏差。稳定误差的大小反映了系统对给定输入的跟踪精度和抗干扰能力。

标签:稳定误差，定义，影响因素

二、二次系统稳定误差的影响因素

1.系统的结构:二次系统的结构决定了系统的动态特性和稳态性能。稳定误差取决于系统的结构。

2.控制器参数:控制器参数的设置直接影响系统的稳态误差。合理的控制器参数可以减小稳态误差。

3.输入信号:输入信号的形式和大小也会影响稳态误差。例如，步进输入信号和斜坡输入信号对稳定误差的影响不同。

4.系统参数:系统参数的变化会导致系统动态特性的变化，从而影响稳定误差。

标签:系统结构，控制器参数，输入信号，系统参数。

三、二级系统稳定误差优化策略

1.优化系统结构:通过改进系统结构，提高系统的动态性能和稳态性能，从而减少稳态误差。

2.控制器参数优化:合理设置控制器参数，在系统稳定过程中消除小的稳态误差。

3.输入信号的优化:根据实际需要，选择合适的输入信号形式，减少稳定误差。

4.优化系统参数:通过调整系统参数，使系统在稳定运行过程中存在小的稳定状态误差。

标签:系统结构优化，控制器参数优化，输入信号优化，系统参数优化

四、案例分析

作为典型的二次系统的例子，分析稳定误差的最优化策略。采用PID控制器，输入信号为步进信号。通过优化系统结构、控制器参数、输入信号、系统参数，降低稳态误差。

1.优化系统结构:系统结构由一楼系统改为二楼系统，提高系统动态性能。

2.控制器参数优化:根据ziegler-nichols方法，调整PID控制器参数，使系统在稳定运行过程中稳定误差较小。

3.优化输入信号:将步进信号改为斜坡信号，减少稳态误差。

4.系统参数优化:调整系统参数，在系统稳定运行过程中有小的稳定状态误差。

标签:案例分析，优化策略，系统性能。

五、结论。

本论文详细解析了二阶系统稳定误差的概念，影响因素和优化策略。通过优化系统结构、控制器参数、输入信号和系统参数，可以有效减小二次系统的稳态误差，提高系统性能。

标签:结论，优化策略，系统性能，稳定误差。

二阶系统稳态误差产生的原因

3二次系统稳定误差的原因分析

在自动控制系统中，稳定误差是衡量系统性能的重要指标之一。为了帮助读者更好地理解这一现象，本文将深入探讨二次系统稳定误差产生的原因。

3标签:序言。

稳定误差是指系统达到稳定状态时的输出值与期望值的偏差。二次系统的情况下，稳定误差的产生通常与系统的结构，参数设定，输入信号特性有关。

3标签:对系统结构稳定误差的影响。

二次系统的稳定误差首先与系统的结构有关。典型的二阶系统包括比例(P)、积分(I)和微分(D)环。这里消除稳定误差的关键是积分过程。

如果没有积分环，系统就不能消除稳定误差。形成静差系统。这是因为积分过程可以使稳定时的系统输出值接近期望值，从而消除稳定误差。

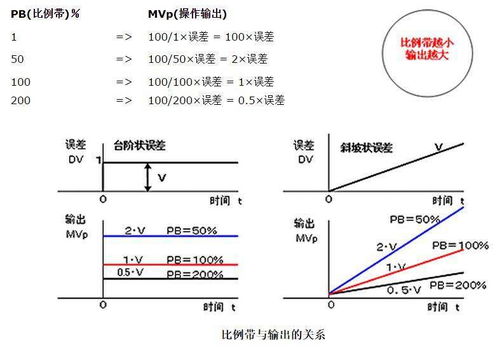
3标签:参数设置对稳定误差的影响。

二次系统的参数设定也会影响稳定误差。主要是衰减比(z)和不衰减的自然振动频率(ω)。

阻尼比决定了系统的响应速度和稳定性。当阻尼比过大时，系统响应速度变慢，稳态误差增大;阻尼小的话，系统容易振动，稳定误差变大。

不衰减的自然振荡频率反映了系统的自然响应特性。当不衰减自然振荡频率过高时，系统响应速度加快，但稳态误差可能增大;没有衰减的自然振荡频率过低的话，系统的响应速度变慢，稳态误差可能变大。

3标签:输入信号特性对稳定误差的影响。

输入信号的特性也是影响二次系统的稳定误差的重要因素。一般的输入信号有步进信号、斜坡信号、正弦信号等。

在步进信号的情况下，二次系统通常可以快速到达稳定状态，稳定误差变小。但对于斜坡信号和正弦波信号，二次系统的稳态性误差可能较大，需要通过调整系统参数或增加积分环节来减小。

3标签:实际因素对稳定误差的影响。

在实际应用中，系统可能存在传感器误差、执行器误差、噪声等实际因素。

传感器误差和执行器误差会在系统输出值和期望值之间产生偏差，产生稳定误差。噪声有使系统输出值变动，增大稳定误差的可能性。

3标签:总结

二次系统稳态误差的原因主要包括系统结构、参数设置、输入信号特性和实际因素等。理解这些原因有助于稳定误差问题的分析和解决，提高自动控制系统的性能。

在实际应用中，应根据具体情况选择适当的系统结构、参数设置和输入信号，并采取措施以减少实际因素的影响，从而降低稳态误差，使系统的提高性能。

二型系统稳态误差

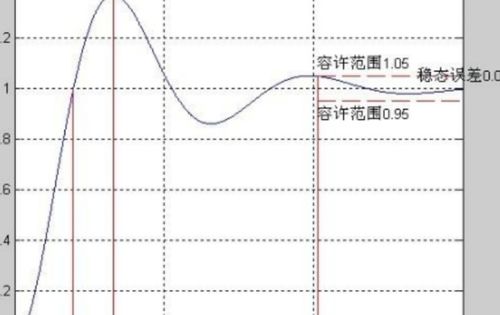
3二型系统稳定误差的分析和优化策略。

随着自动化技术的不断发展，2型系统在工业控制领域得到了广泛应用。二型系统，即具有两输入两输出的系统，因其独特的结构特点，在处理复杂的控制问题时具有显著的优越性。二型系统在运行过程中可能出现稳态误差，影响系统的控制精度和稳定性。本论文探讨二型系统稳定误差的分析和优化策略。

标签:二型系统，稳定误差，分析，优化策略

3一、二型系统的稳定误差分析

二型系统稳定误差是指系统在稳定运行过程中，输出信号与期望信号之间的偏差。稳定误差的产生主要与以下因素有关。

系统结构:2型系统结构复杂，输入输出关系复杂，容易产生稳态误差。

系统参数:系统参数设置不合理会导致稳态误差增大。

干扰:噪声、负载变化等干扰会影响系统的稳定性能。

控制器的设计:控制器的设计不合适的话稳态误差会变大。

3二、二型系统稳定误差的最优化策略。

针对二型系统的稳定误差问题的最优化策略如下所示。

优化系统结构:通过合理设计系统结构，降低系统输入输出关系的复杂性，从而减小稳态误差。

系统参数优化:根据系统特性和实际需求，合理设置系统参数，减少稳态误差。

抑制扰动:采用过滤、抗干扰等技术，降低扰动对系统的影响，提高系统稳定性。

优化控制器设计:采用先进的控制器设计方法，采用自适应控制、鲁棒控制等，提高系统控制的精度和稳定性。

3 3，实例分析。

下面，为了说明优化系统稳定误差的方法，以简单的类型2的系统为例。

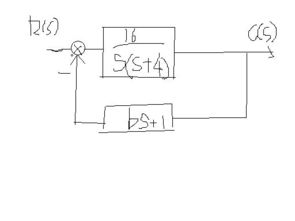
假设两种系统由两个输入信号u1和u2以及两个输出信号y1和y2构成。系统构成如下所示。

![]系统结构图(https://example.com/system_structure.pg)

根据系统结构，系统传递函数可以列举如下。

$ $ g (s) = frac {y1 (s)}{决定为u1 (s)} = frac {y2 (s)} {u2 (s)} = frac所属k1} {{s ^ 2 + 2zetaomega _somega _^ 2} $ $

其中，K1是系统增益，ω是自然频率，z是阻尼比。

为了减小稳定误差，可以采取以下措施。

优化系统参数:通过调整K1、ω、z，使系统具有适当的阻尼比和自然频率，从而降低稳态误差。

优化控制器设计:采用PID控制器，可根据系统特性调整尺度、积分、微分参数，提高系统控制精度和稳定性。

3第四结论

二型系统稳态误差是影响系统性能的重要因素。通过对系统结构、参数、干扰和控制器设计的优化，可以有效减少两种系统的稳态误差，提高系统的控制精度和稳定性。在实际应用中，根据具体的系统特性和需求，采取最优化的策略，实现最佳的控制效果。

3标签:二型系统，稳定误差，优化，示例分析

系统稳态误差的计算例题

3系稳定误差计算例题详解

在自动控制系统中，稳定误差是衡量系统性能的重要指标之一。这里用具体的例题详细说明系统稳定误差的计算方法。

标准:系统稳定误差，计算方法，例题分析

一、序言。

稳定误差是指系统达到稳定状态后的实际输出与期望输出之间的偏差。稳定误差的计算对于评估系统的控制精度和性能很重要。在此以一般的计算方法为例，通过具体的例题来详细介绍。

3 2，问题的背景。

假设有控制系统。开环传递函数是(G(s) = frac{200}{s(s+2)(s-10)})。这里计算输入信号为(R(s) = frac{1}{s})(单位斜坡信号)时系统的稳定误差。

3三，稳定误差的计算。

计算稳定误差首先需要确定系统的种类从开环传递函数可知，系统包含纯积分环，因此是二阶系统。

3 4，确定误差系数。

在二次系统中，稳定误差可以用下面的公式计算。[ess = frac{1}{k_v}]其中(k_v)是速度误差系数。[k_v = lim_{so 0} sG(s)]将(G(s))代入这个公式，得到如下。[k_v = lim_{s0} s dot frac{200}{s(s+2)(s-10)} = frac{200}{2dot 10} = 10]3 5，计算稳定误差。

因为得到了速度误差系数(k_v = 10)，所以可以计算稳定误差。[ess = frac{1}{k_v} = frac{1}{10} = 0.1]，因此输入为单位斜坡信号时，系统的稳定误差为0.1。3 6，总结

前面的例题详细讲解了如何计算系统的稳定误差。确定系统类型，计算速度误差系数(k_v)，最后使用稳定误差公式计算。这种方法适用于各种类型的控制系统，是控制系统分析的基本技能。

3第七注意事项

计算稳定误差时，需要注意以下几点。

确认系统处于稳定状态。正确识别系统类型使用正确的公式和计算方法。3 8，结论

本文将通过具体例题，详细介绍系统稳定误差的计算方法。掌握这一技能对于控制系统的设计和分析具有重要的意义。通过不断的练习和我们可以提高在控制系统领域的工作能力。