电力系统分析节点导纳矩阵试题,电力系统分析节点导纳矩阵例题

电力系统分析节点导纳矩阵试题目录

电力系统分析节点导纳矩阵试题

电力系统分析节点导纳矩阵例题

电力网络的节点导纳矩阵

节点导纳矩阵阶数与电力系统节点数关系如何

电力系统分析节点导纳矩阵试题

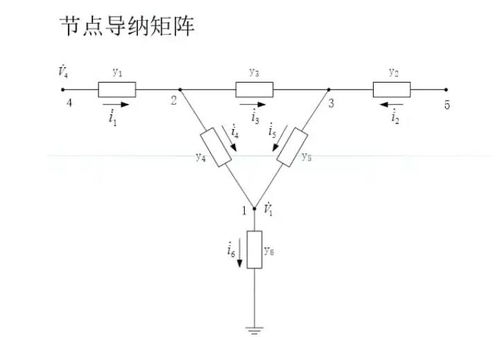
电力系统分析节点导纳矩阵测试

标签:电力系统分析，节点导纳矩阵，试题解析。

在电力系统的分析中，节点导矩阵是一个非常重要的工具，有助于理解和计算电力系统中各节点之间的电气特性。下面是一篇关于电力系统分析节点的导纳矩阵问题的文章，旨在帮助读者更好地理解和解决问题。一、试题的背景

标签:问题背景，电力系统分析

电力系统分析是电气工程领域的基础科目之一，节点导矩阵是电力系统分析的核心内容。在电力系统分析中，节点导电矩阵用于描述电力系统中各节点之间的导电性参数，是潮流计算、短路分析、电压稳定性分析、网络规划等的重要依据。二、试题内容

标签:问题内容，节点引导矩阵

以下是关于节点的导纳矩阵的问题:问题:已知的电力系统包括以节点1为参考节点的5个节点。系统是以下的绕行参数包括:2 | |支路号码1 | |ノードノードインピーダンス(欧米伽)电纳(s) | ||————————————————————|——|————————————————————————|———————————|———————————| 1 | | | 2 | 100.5 | | | .3 | 2 | 135 | | | || 31 | 4 | 8 | .22 | | | | 4 . 45 | 6 | | | | 53 | 5 | 4 | .1 |请该电力系统的计算ノードアドミッタンス行列。三、试题解析

标签:问题解析，节点导纳矩阵计算

要计算节点导引矩阵，需要知道节点导引矩阵的构成。节点微分矩阵是N×N的复数矩阵，N是电力系统中节点的数量。矩阵的元素Yij表示节点i和节点j之间的推导(即Yij = Gij + jBij)。这里，Gij是电导，Bij是电推导。赋予问题的分歧参数开始,我们以下的节点导纳队伍一样可以计算:| | 11 | y y 12 y | 15 | 14 | 13 | y y| - - - - - - - - | - - - - - | - - - - - | - - - - - | - - - - - | - - - - - | | y21 | | y22 | y23 | y24 | y25 | | y31 | | | y33 | y34 |y35 | | y41 | | | | y44 | y45 | | y51 | | | | | y55 |中,y11 = g11 + jb11苏莎12 y = g12 + jb12,类推。根据问题中给出的旁路参数，我们可以计算出以下的值:- Y11 = 0 + j0 = 0- Y12 = 0.5 + j0 = 0.5- Y13 = 0.3 + j0 =0.2 + j0 = 0.2- Y15 =0 + j0 =0 - Y21 =0.5 + j0 =0.5- Y22 =0 + 0- Y23 =0 + j0 =0 - Y24 = 0.2 +j0 = 0- Y25 = 0 +j0 = Y31 = 0.3 +j0 = 0.3- Y32 = 0.3 +j0 = 0.3- Y33 = 0 +j0 = 0- Y34 = 0.2 +j0 =0.2 - Y35 =0 + j0 =0 - Y41 =0.2 + j0 =0.2 - Y42 =0.2 + j0 =0.2 - Y43 =0.2 + j0 =0.2 - Y44 =0+ j0 = 0- Y51 = 0 + j0 = 0- Y52 = 0 + j0 = 0- Y53 = 0 + j0 = 0- Y54 = 0 + j

电力系统分析节点导纳矩阵例题

3电力系统分析节点导纳矩阵例题详解

在电力系统的分析中，节点导矩阵是一个非常重要的工具，有助于理解和计算电力系统中各节点之间的电气特性。本文通过具体的例题，详细解析节点导纳矩阵的形成过程及其在电力系统分析中的应用。

电力系统解析，节点导纳矩阵，例题解析

一、例题的背景。

假设有一个简单的电气系统，由3个节点和4个旁路组成，节点号分别是1、2、3，旁路号分别是1、2、3、4。每个旁路的电阻和导电情况如下表所示。

支路编号电阻(欧米茄)电纳(s) 1 100.1 2 5 0.05 3.15 0.15 4 20 0.23 2，形成节点导纳矩阵。

节点导出矩阵是x的复数矩阵，是电气系统中节点的数量。每个元件Yij表示节点i和节点j之间的导电性，导电性(G)和电的导电性(B)的复数。

需要计算各个旁路的向导Y的计算公式如下。

Y = 1 / (G + jB)。

根据上述公式，我们可以计算每个旁路如下:

旁路编号指南(S) 1 0.1 + j0.01 2 0.2 + j0.01 3 0.0667 + j0.0054 0.05 + j0.01接下来。根据分支指南，需要填写节点指南矩阵。节点微分矩阵有如下规则。

对角线元素Yii表示节点i的自传导性，即节点i和其自身之间的传导性。非对角线元素Yij表示节点i和j之间的相互传导性，即节点i和j之间的相互传导性。根据这些规则，节点微分矩阵可以写成如下。

Y11 Y12 Y13 Y11 0.1 +j0.01 -0.1 - j0.01 -0.0667 - j0.005 Y12 -0.1 - j0.01 0.2 +j0.01 -0.0667 -j0.005 Y13 -0.0667 - j0.005 -0.0667 + j0.005 3 3，节点微分矩阵的应用。

node guide矩阵在电力系统的分析中被广泛使用。以下是一般的应用例子。

电力网络的节点导纳矩阵

3电力网络节点的导纳矩阵:概念、应用和计算方法

在电力系统分析中，节点导电矩阵是描述电力系统中各节点之间的导电性参数和导电性参数的重要工具。这里详细说明节点微分矩阵的概念、应用和计算方法。

3概念。

3一、节点导纳矩阵的基本概念

节点导出矩阵是维x的复数矩阵，是电力系统中节点的数量。矩阵的各要素表示节点间的导电性，导电性是电导和电导的复数。电导表示电流容易通过，电纳米表示电流难通过。

节点导出矩阵的主对角线元素被称为自导，包括节点上的总电导和电导。不是主对角线的元件被称为互传导，表示节点间的电流耦合效果。

3标签:应用程序

3 2，节点导纳矩阵的应用领域。

节点导向矩阵被广泛用于电力系统的分析。

潮流分析:通过节点导数矩阵，可以计算电力系统各节点的电压和电力潮流，评价电力系统的稳定性和负荷分布。

短路分析:计算短路电流，确保系统设备和电缆能承受短路条件下的电流。

电压稳定性分析:分析电压的稳定性，保证电压在允许范围内。

网络规划:对新建电力线、变电站、电站进行性能评估。

3标签:计算方法

3 3，节点导纳矩阵的计算方法。

节点微分矩阵可以通过以下步骤计算:

建立网络拓扑矩阵:根据电力网络的连接关系和元件特性，建立相关矩阵来描述分支和节点之间的关系。

节点导数的计算:从网络拓扑矩阵计算每个节点的自导数和互导数。

建立节点微分矩阵:将计算出的自微分和互微分放入节点微分矩阵中。

3标签:实例分析。

3 4，节点导纳矩阵的例子的分析。

以下是有5个节点和5个旁路的电力网络的节点微分矩阵的计算例子。

节点1y11, Y12, Y13, Y14是互连节点。Y15节点2y21, Y22, Y23, Y24, Y25节点3y31, Y32, Y33，Y34,Y35节点4y41 Y42, Y43, Y44, Y45节点5y51 Y52, Y53, Y54,Y55 3标记:总结

3 5，总结

节点导轨矩阵是分析电力系统不可或缺的工具，可以帮助我们了解电网的电气特性，确保电力系统的可靠性和安全性。本文介绍节点导纳矩阵的概念、应用和计算方法，以便给电力系统工程师提供有益的参考。

节点导纳矩阵阶数与电力系统节点数关系如何

3节点微分矩阵的阶数和电力系统节点数的关系。

在电力系统分析中，节点导矩阵是了解和计算电力系统运行状态的一个非常重要的工具。本论文探讨了节点微分矩阵的阶数和电力系统节点数的关系，并说明了其背景。

3标记:节点微分矩阵。

3节点的导纳矩阵是什么?

节点感应矩阵是电力系统分析中的方阵之一，用于描述系统中每个节点之间的感应关系。导体用阻抗的倒数测量流过节点的电流流动。节点导引矩阵的每个元素表示两个节点之间的导引值，自导引对应于节点自身的导引值，互导引表示两个不同节点之间的导引值。

3标签:电力系统的节点数。

3电力系统的节点数量对节点导引矩阵的影响。

电力系统的节点数直接决定了节点导矩阵的阶数。具体来说，如果某个电力系统中有节点，那么该节点导出矩阵的阶数如下。这是因为节点的导引矩阵是包含所有节点之间的导引关系的×方阵。节点的数量越多，节点微分矩阵的规模也就越大，计算的复杂度也就越高。

3标记:矩阵的阶数。

3节点微分矩阵的阶数和矩阵特征

节点微分矩阵有如下特征。

方阵:节点引导矩阵是行数和列数相等，等于节点数的方阵。对称矩阵:节点微分矩阵是对称的，矩阵的元素满足a[i][j] = a[j][i]，其中a[i][j]代表第i行第j列的元素。稀疏矩阵:在节点的引导矩阵中，几乎所有的元素都是零，因为并不是所有节点都有直接的引导关系。这种稀疏性提高了矩阵的保存和计算的效率。3标签:复杂性。

3节点微分矩阵的阶数和计算复杂度的关系。

随着节点微分矩阵的阶数增加，计算的复杂度也会增加。这是因为矩阵的各个要素都需要复杂的计算。特别是电力系统的稳定分析和动态分析的情况。例如，在潮流计算中，为了解电力系统的电力分布，节点导矩阵被使用。节点的数量越多，求解这个方程式所需要的计算资源也就越多。

3标准:电力系统分析

3节点导纳矩阵在电力系统分析中的应用

节点导向矩阵在电力系统的分析中起着重要的作用。以下是主要的应用例子。

潮流计算:根据节点导数矩阵，可以计算出电力系统各节点的电压和电流分布。稳定性分析:节点导矩阵有助于评估电力系统的稳定性。通过分析矩阵的特征值和特征向量，可以预测系统的动态行为。故障分析:电力系统发生故障时，节点?导游?矩阵可以帮助我们分析故障对系统造成的影响，并制定相应的恢复策略。3标签:总结

3总结节点微分矩阵的阶数和电力系统节点数的关系。

节点微分矩阵的阶数与电力系统的节点数直接相关。节点的数量增加的话，节点微分矩阵的阶数也会增加，计算的复杂度也会增加。节点导向矩阵在电力系统分析中发挥着不可替代的作用，可以帮助我们更好地理解和预测电力系统的工作状态。因此，虽然增加了计算复杂度，但节点导出矩阵仍然是分析电力系统不可或缺的工具。