dft三大系统,离散傅里叶变换

离散傅里叶变换（Discrete Fourier Transform，DFT）作为一种重要的数学工具，在信号处理、图像处理、通信系统等领域有着广泛的应用。DFT的三大系统，即DFT、逆DFT（IDFT）和快速傅里叶变换（FFT），是理解和应用DFT的基础。本文将详细介绍这三大系统，并探讨它们在各个领域的应用。

DFT：离散傅里叶变换

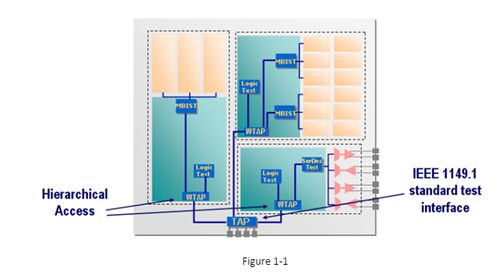
DFT是一种将时域信号转换为频域信号的方法。它将一个离散的时域信号分解为若干个不同频率的正弦波和余弦波的线性组合。DFT的计算公式如下：

[ X[k] = sum_{n=0}^{N-1} x[n] cdot e^{-frac{2pi jkn}{N}} ]

其中，( X[k] ) 是频域信号，( x[n] ) 是时域信号，( N ) 是信号长度，( j ) 是虚数单位。DFT在信号处理中具有重要作用，如频谱分析、滤波、调制等。

IDFT：逆离散傅里叶变换

IDFT是将频域信号转换回时域信号的方法。它是DFT的逆变换，计算公式如下：

[ x[n] = frac{1}{N} sum_{k=0}^{N-1} X[k] cdot e^{frac{2pi jkn}{N}} ]

IDFT在信号处理中同样具有重要作用，如解调、反滤波等。通过IDFT，我们可以从频域信号中恢复出原始的时域信号。

FFT：快速傅里叶变换

FFT是一种高效的DFT算法，它将DFT的计算复杂度从 ( O(N^2) ) 降低到 ( O(N log N) )。FFT的原理是将DFT分解为多个较小的DFT，从而减少计算量。FFT在信号处理中具有广泛的应用，如实时信号处理、图像处理等。

FFT的算法有多种，如Cooley-Tukey算法、Butterfly算法等。其中，Cooley-Tukey算法是最常用的FFT算法，它将DFT分解为两个大小减半的DFT，然后通过合并这两个DFT来计算最终的DFT。

三大系统在各个领域的应用

DFT、IDFT和FFT在各个领域都有广泛的应用，以下列举一些典型应用：

信号处理

在信号处理领域，DFT、IDFT和FFT被广泛应用于频谱分析、滤波、调制、解调等。例如，在无线通信中，FFT用于调制和解调信号，以提高通信效率。

图像处理

在图像处理领域，DFT、IDFT和FFT被广泛应用于图像压缩、图像增强、图像恢复等。例如，JPEG图像压缩算法就是基于DFT的。

通信系统

在通信系统领域，DFT、IDFT和FFT被广泛应用于信号调制、解调、信道编码、信道解码等。例如，在数字电视广播中，FFT用于调制和解调信号。

其他领域

DFT、IDFT和FFT在其他领域也有应用，如控制理论、生物信息学、金融工程等。

DFT、IDFT和FFT是离散傅里叶变换的三大系统，它们在信号处理、图像处理、通信系统等领域具有广泛的应用。通过本文的介绍，读者可以了解到这三大系统的基本原理和应用场景，为在实际工作中应用DFT提供参考。

DFT IDFT FFT 离散傅里叶变换 信号处理 图像处理 通信系统 快速傅里叶变换