0阻尼系统,什么是0阻尼系统？

什么是0阻尼系统？

0阻尼系统，也称为无阻尼系统，是一种理想化的物理系统，其中阻尼系数为零。在现实世界中，所有系统都存在一定的阻尼，它反映了系统在运动过程中能量耗散的程度。然而，在理论研究和工程应用中，为了简化问题，有时会忽略阻尼的影响，将其视为0阻尼系统。

0阻尼系统的特点

0阻尼系统的特点主要体现在以下几个方面：

自由振动：0阻尼系统在受到外力作用后，会进行自由振动，即系统在无外力作用下，依靠自身的惯性继续运动。

振动频率：0阻尼系统的振动频率等于其固有频率，固有频率是系统在无阻尼情况下的自然振动频率。

振幅：0阻尼系统的振幅在理论上会无限增大，但在实际应用中，由于系统受到外界因素的限制，振幅会趋于稳定。

0阻尼系统的应用

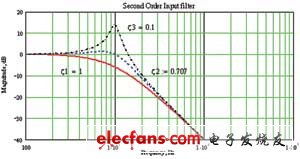
0阻尼系统在理论研究和工程应用中具有重要意义，以下列举几个应用场景：

振动分析：在研究机械结构、建筑结构等系统的振动特性时，可以将系统视为0阻尼系统，从而简化计算过程。

控制系统设计：在控制系统设计中，0阻尼系统可以用于分析系统的稳定性和动态性能。

信号处理：在信号处理领域，0阻尼系统可以用于研究信号的频谱特性。

0阻尼系统的局限性

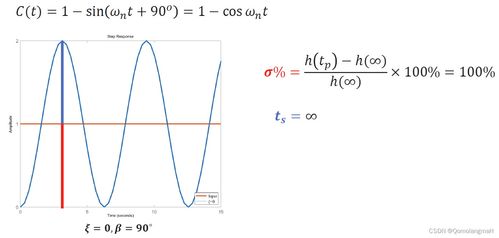
尽管0阻尼系统在理论研究和工程应用中具有重要意义，但其也存在一定的局限性：

理想化：0阻尼系统是一种理想化的模型，与实际系统存在一定的差距。

计算复杂：在0阻尼系统中，系统的运动方程和传递函数较为复杂，计算过程相对繁琐。

实际应用受限：由于实际系统中存在阻尼，0阻尼系统在实际应用中存在一定的局限性。

0阻尼系统的实例分析

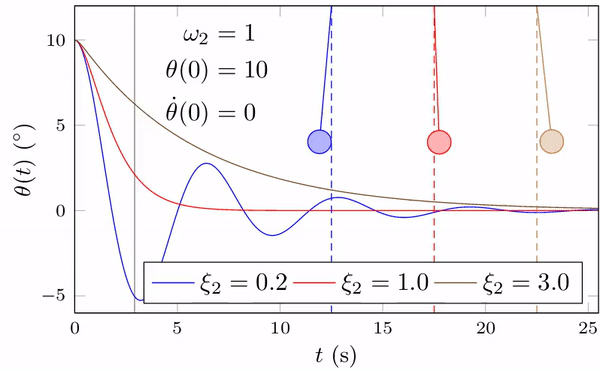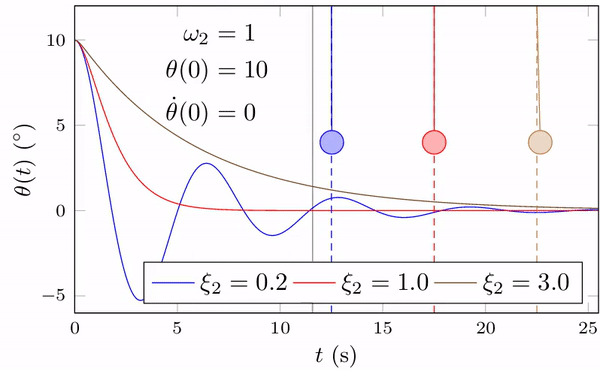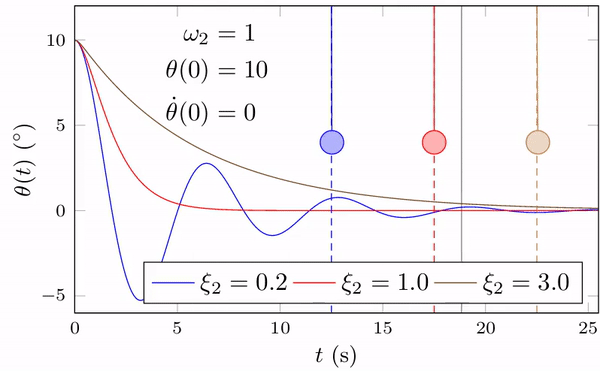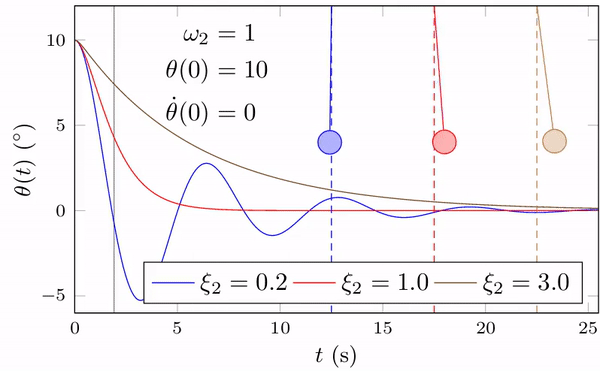
以下以一个简单的单自由度弹簧-质量系统为例，分析0阻尼系统的运动特性。

假设系统由一个质量为m的物体和一个刚度为k的弹簧组成，系统受到一个外力F(t)的作用。根据牛顿第二定律，系统的运动方程可以表示为：

mfrac{d^2x}{dt^2} + kx = F(t)

当阻尼系数c=0时，该方程简化为：

mfrac{d^2x}{dt^2} + kx = F(t)

该方程的解为：

x(t) = C_1cos(sqrt{frac{k}{m}}t) + C_2sin(sqrt{frac{k}{m}}t) + frac{F(t)}{k}

其中，C_1和C_2为积分常数，由初始条件确定。

0阻尼系统是一种理想化的物理系统，在理论研究和工程应用中具有重要意义。然而，在实际应用中，由于实际系统中存在阻尼，0阻尼系统存在一定的局限性。了解0阻尼系统的特点、应用和局限性，有助于我们更好地理解和分析实际系统。