2阶系统,什么是2阶系统？

什么是2阶系统？

2阶系统是一种常见的动态系统，它在数学模型中通常表示为二阶微分方程。这类系统在物理学、工程学、经济学等多个领域都有广泛的应用。2阶系统的主要特点是包含两个独立的状态变量，并且其动态行为可以通过两个微分方程来描述。

2阶系统的数学模型

一个典型的2阶系统可以用以下微分方程来表示：

[ ddot{x}(t) + adot{x}(t) + bx(t) = f(t) ]

其中，( x(t) ) 是系统的状态变量，( ddot{x}(t) ) 是状态变量的加速度，( dot{x}(t) ) 是状态变量的速度，( a ) 和 ( b ) 是系统参数，( f(t) ) 是外部激励或输入。

2阶系统的特性

2阶系统的特性主要包括以下几个方面：

阻尼比：阻尼比是衡量系统阻尼特性的参数，通常用 ( zeta ) 表示。阻尼比的大小决定了系统的响应速度和稳定性。当 ( zeta 1 ) 时，系统为过阻尼。

自然频率：自然频率是系统在没有外部激励时的固有频率，通常用 ( omega_n ) 表示。自然频率决定了系统的振荡频率。

衰减系数：衰减系数是描述系统响应衰减速度的参数，通常用 ( alpha ) 表示。衰减系数与阻尼比和自然频率有关。

2阶系统的响应分析

2阶系统的响应分析主要包括以下几种情况：

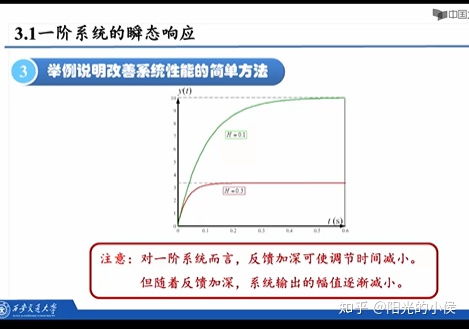
欠阻尼响应：当系统为欠阻尼时，其响应将呈现振荡衰减的趋势，最终趋于稳定。

临界阻尼响应：当系统为临界阻尼时，其响应将迅速趋于稳定，没有振荡过程。

过阻尼响应：当系统为过阻尼时，其响应将缓慢趋于稳定，没有振荡过程。

2阶系统的应用

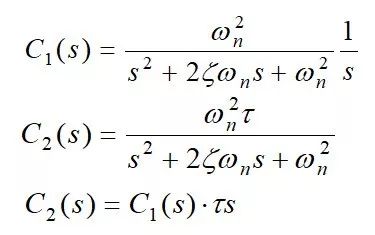
2阶系统在各个领域都有广泛的应用，以下列举一些常见的应用场景：

机械系统：如弹簧-阻尼器系统、振动台等。

控制系统：如伺服电机、PID控制器等。

生物系统：如心脏跳动、呼吸运动等。

经济系统：如投资回报、经济增长等。

2阶系统的设计

在设计2阶系统时，需要考虑以下因素：

系统参数的选择：根据实际需求选择合适的阻尼比、自然频率等参数。

外部激励的处理：合理设计外部激励，以满足系统性能要求。

系统稳定性分析：确保系统在运行过程中保持稳定。

2阶系统作为一种常见的动态系统，在各个领域都有广泛的应用。通过对2阶系统的数学模型、特性、响应分析等方面的研究，可以更好地理解和设计这类系统，以满足实际需求。随着科学技术的不断发展，2阶系统的研究和应用将越来越广泛。